فصل ۷: اعداد فیبوناچی، تاریخچه و کارایی

• اعداد صحیح و اعداد فیبوناچی
• تاریخچه اعداد فیبوناچی
• نسبت طلایی
• نسبت های فیبوناچی
• اعداد فیبوناچی در طبیعت
• اعداد فیبوناچی و دلایل اهمیت
• فیبوناچی در بازارهای مالی
• فیبوناچی در امواج
• مورد اول: فیبوناچی اصلاحی یک موج جنبشی
• مورد دوم: فیبوناچی برای دو موج

 اعداد صحیح و اعداد فیبوناچی

اعداد صحیح

اعداد صحیح مجموعه اعداد طبیعی، صفر و قرینه اعداد طبیعی هستند که ترتیب آنها اختلافی از عدد یک است. این اعداد شناخته شده ترین و ساده ترین پایه ریاضیات هستند.

سری اعداد صحیح شامل:

اعداد طبیعی

...و۱,۲,۳,۴,۵,۶,۷,۸,۹,۱۰,۱۱,۱۲

عدد صفر:

۰

قرینه اعداد طبیعی:

...,۱۲-,۱۱-,۱۰-,۹-,۸-,۷-,۶-,۵-,۴-,۳-,۲-,۱-

اعداد صحیح برای محاسبه و شناخت سری اعداد تکی کاربرد دارند.

تاریخچه اعداد فیبوناچی

در قرن سیزدهم در روم (ایتالیای کنونی) که در آن زمان مهد ریاضیات محسوب می شد پادشاه روم فردریک دوم معمایی مطرح کرد و برای کسی که این معما را حل کند جایزه نفیسی در نظر گرفت. این معما توسط لئوناردو فیبوناچی ریاضیدان آن زمان که در شهر پیزای روم زندگی می کرد حل گردید و روش حل این معما پایه اعدادی شد که به نام خود او اعداد فیبوناچی نامگذاری شدند.

سوال معما این بود:

در یک محیط بسته طی مدت یک سال، چند جفت خرگوش می توان از یک جفت خرگوش تولید کرد، اگر هر جفت در هر ماه یک جفت دیگر به دنیا آورد و هر جفت تولید مثل را از ماه دوم زندگی خود آغاز کند؟

فیبوناچی معمای پادشاه روم را توسط رشته اعدادی به هم پیوسته حل کرد که طبق نظم خاصی به هم مرتبط بودند این اعداد به نام اعداد فیبوناچی نامگذاری شدند و بعدها کاربرد بسیار وسیعی پیدا کردند.

ترتیب اعداد فیبوناچی:

...,۱,۱,۲,۳,۵,۸,۱۳۳,۲۱,۳۴,۵۵,۸۹,۱۴۴,۲۳۳

در این سری اعداد فیبوناچی هر عدد مجموع دو عدد قبلی خود است و مبنای شروع آن ابتدای اعداد صحیح است.

حال اگر به معمای پادشاه برگردیم و در سری فیبوناچی هر عدد را برای یک ماه در نظر بگیریم می بینیم که جواب معما ۱۴۴ عدد خرگوش بعد از ۱۲ ماه است.

نسبت طلایی

اگر به استثنای چند عدد اول به نسبت اعداد فیبوناچی به همدیگر دقت کنیم متوجه یک عدد ثابت در تمام این مجموعه می شویم

نسبت عدد کوچکتر به بزرگتر:

۰٫۶۲=۵/۳

۰٫۶۱۸=۲۱/۳۴

۰٫۶۱۸=۵۵/۸۶

نسبت ۰٫۶۱۸ در اعداد فیبوناچی را عدد فی هم می گویند. نسبت عدد بزرگتر به عدد کوچکتر عدد ۱٫۶۱۸ است. فی تنها عددی است که وقتی با یک جمع می شود حاصل آن معکوس آن است:

۰٫۶۱۸+۱=۱٫۱۶۱۸=۱/۰٫۶۱۸

نسبت های فیبوناچی

نسبت های دیگر: نسبت اعداد یک در میان به هم ۰٫۳۸ و ۲٫۶۱ است.

۰٫۳۸=۵۵/۱۴۴

۲٫۶۱=۱۴۴/۵۵

این نسبت ها بین تمام اعضای یک در میان اعداد فیبوناچی برقرار است.

اعداد فیبوناچی در طبیعت

کارایی اعداد فیبوناچی در خلق کائنات و اعضای بدن موجودات قابل مشاهده هستند (شکل ۱۰۷). در ساختارهایی مانند:

• هر نوع مارپیچ حلزونی ساخت طبیعت مانند لاک حلزون یا اسپیرال گوش موجودات
• نسبت دانه های گل آفتابگردان
• میوه درخت کاج
• اسپیرال یا مارپیچ کهکشان راه شیری
• چرخش گردباد و گرداب ها
• نسبت چرخش رشته های مارپیچ DNA
• نت های موسیقی
• ساختار مولکولی
• سلول های عصبی
• ساختار کریستال
• شکست نور در شیشه

به عدد فی و نسبت عکس آن نسبت طلایی و نسبت پایه و مبنای خلق جهان آفرینش می گویند.

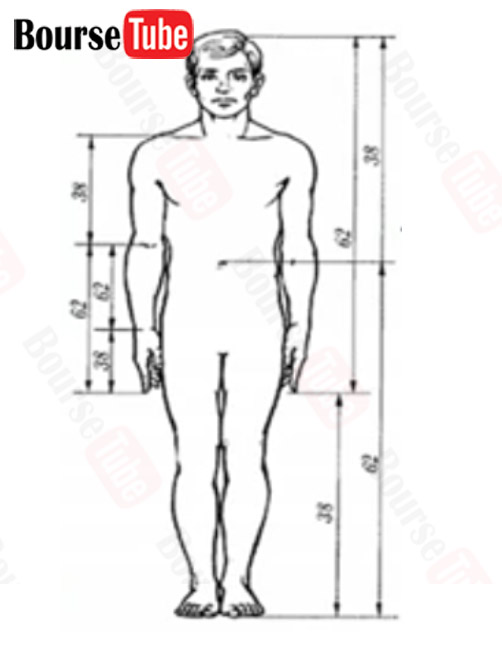
شکل ۱۰۷: نسبت طلایی در بدن انسان

اعداد فیبوناچی و دلایل اهمیت

در اعداد صحیح ارتباط یک عدد فقط با عدد قبلی یا بعدی خود با اختلاف یک وجود دارد و به جز این ارتباط و تناسب دیگری بین اعداد صحیح نیست. ولی در اعداد فیبوناچی هر عدد با اعداد قبل و بعد از خود هر چقدر هم دور از هم باشند تناسب هارمونیکی دارد و این تناسب باعث ایجاد یک پیوستگی معنادار بین همه اعداد آن می شود. در ابتدای زنجیره اعداد فیبوناچی دو عدد یک وجود دارد که این دو «یک» نماد یک جفت هستند.

 فیبوناچی در بازارهای مالی

در بازارهای مالی اعداد فیبوناچی به دو دلیل حایز اهمیت هستند:

دلیل اول: بازارهای مالی اجتماعی از افراد مختلف و سرمایه ها به صورت اجتماع و کلونی هستند.

دلیل دوم: در بازارهای مالی کالاها به صورت جفت ارائه می شوند، یا به صورت پول در مقابل پول مثل فارکس یا به صورت سهام یا کالا در مقابل پول.

 فیبوناچی در امواج

تاثیر نسبت های فیبوناچی در امواج قیمت به صورت های مختلف واقع می شود که دو مورد از مهمترین اثرات آن به شکل زیر است:

مورد اول: فیبوناچی اصلاحی یک موج جنبشی

فیبوناچی اصلاحی یک موج جنبشی خود شامل دو قسمت است:

الف) استفاده از اعداد فیبوناچی در به دست آوردن انتهای امواج اصلاحی داخلی یک موج جنبشی و نقاط برگشت قیمت به سمت جهت قبلی موج اصلی (شکل ۲۰۷)

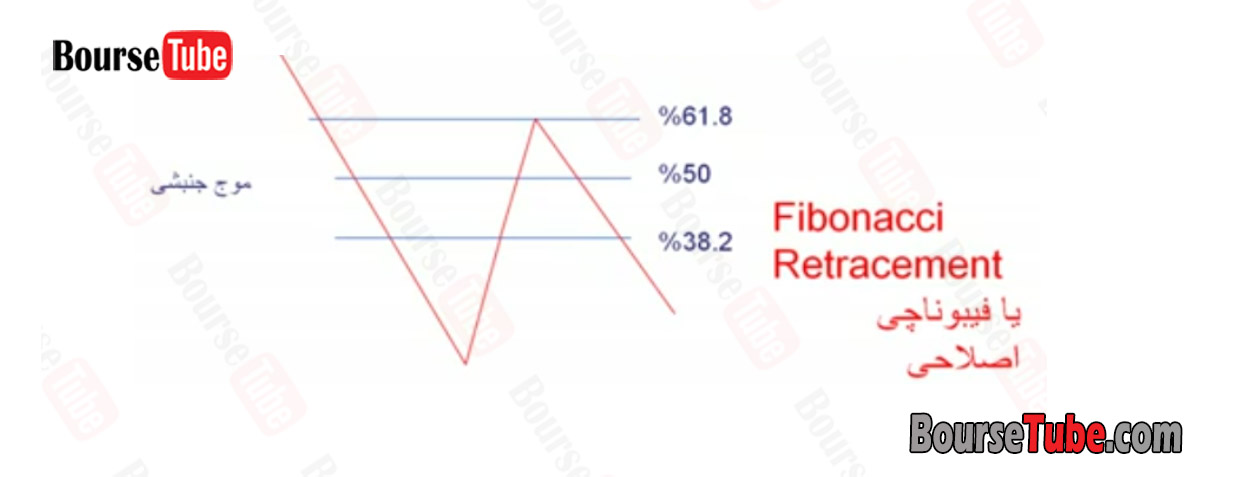
شکل ۲۰۷: فیبوناچی اصلاحی داخلی

یک موج جنبشی یک موج اصلاحی داخلی عموما تا یکی از سطح های شکل ۲۰۷ اصلاح شده و به مسیرش ادامه می دهد. به این نوع فیبوناچی اصلاحی یا Fibonacci Retracement گفته می شود.

ب) استفاده از اعداد فیبوناچی در به دست آوردن انتهای امواج خارجی یک موج و نقاط برگشت قیمت به سمت جهت موج قبلی (شکل ۳۰۷). یک موج اصلاحی خارجی تا یکی از سطوح شکل ۳۰۷ اصلاح شده و به مسیرش ادامه می دهد. به این نوع فیبوناچی امتدادی یا Fibonacci extension گفته می شود.

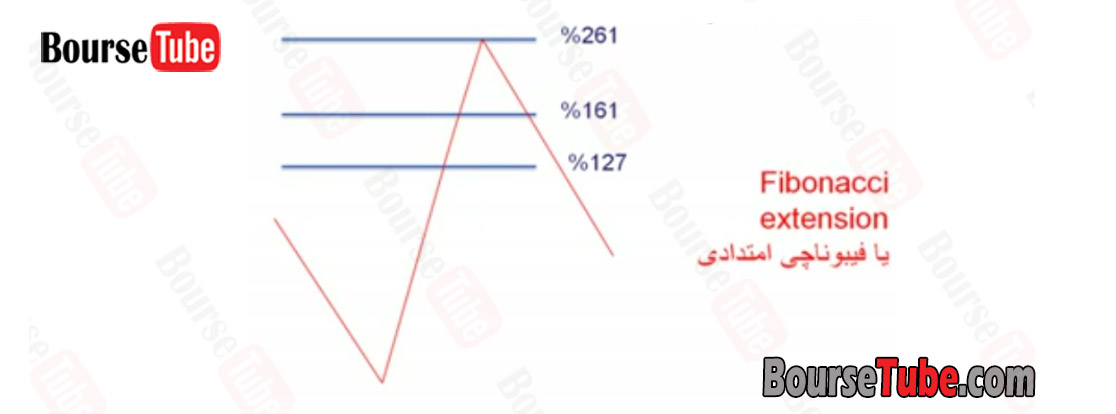
شکل ۳۰۷: فیبوناچی اصلاحی خارجی یک موج جنبشی

جنبشی در متاتریدر برای به دست آوردن انتهای موارد «الف» و «ب» از ابزار Fibonacci Retracement استفاده میکنیم.

مورد دوم: فیبوناچی برای دو موج

شکل ۴۰۷: فیبوناچی اصلاحی دو موج

تا اینجا استفاده از ابزار فیبوناچی برای به دست آوردن نقاط برگشت مربوط به یک موج بود. استفاده از فیبوناچی برای به دست آوردن نقاط برگشت دو موج به هم پیوسته هم بسیار پرکاربرد است که به آن فیبوناچی پروجکشن (پروژه) گفته می شود. (شکل ۴۰۷).

ابزار فیبوناچی پروجکشن در متاتریدر Fibonacci Expansion است. در فیبوناچی پروجکشن فرض بر این است که موج سوم با نسبت های فیبوناچی موج اول، از موج دوم منشعب می شود.

از تایم ۱۹ دقیقه و ۴۸ ثانیه این ویدئو آقای گلشاهیان مثال هایی از کاربرد ابزارهای فیبوناچی بر روی چارت را توضیح می دهند.

برای درک بهتر سطوح فیبوناچی و کاربرد آنها لازم است توضیحات آقای گلشاهیان را با دقت زیاد و تمرین و تکرار آنها مشاهده کرد.

یادآوری مجدد: برگشت از سطوح فیبوناچی حتما باید با الگوهای کندل شناسی تائید شود.

همپوشانی فیبوناچی Retracement و فیبوناچی Expansion در یک ناحیه باعث تقویت برگشت از آن ناحیه می شود.

مبحث بعدی

 

فهرست مطالب

 

مبحث قبلی